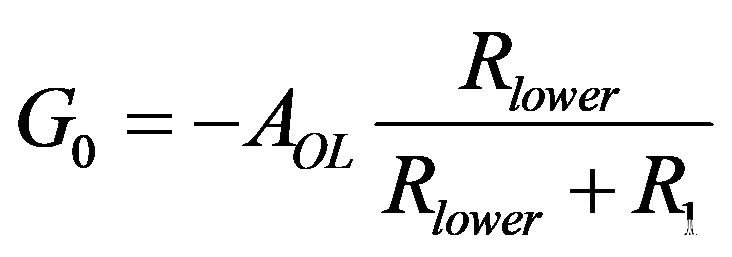发布时间:2020-06-17
阅读量:1718
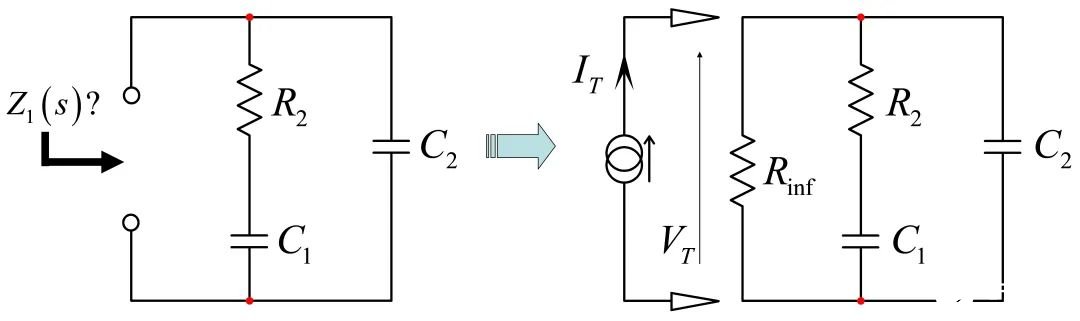
为确定由给出的阻抗,我们可以充分应用所述的快速分析技术。原理图。为了获得阻抗,我们将电流源IT注入到电路环路。IT是激励而VT是响应。我们想要的传递函数是将响应与激励联系起来的关系。为了便于分析,我们在测量终端装上了假负载电阻Rinf。我们将马上看到其中的原理。
有两个电容,这是个二阶电路
这类回路的传递函数可表示为以下形式:
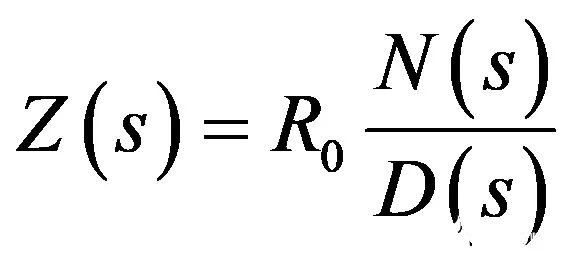
(13)
对于二阶系统,我们可以证明分母遵循下列公式:
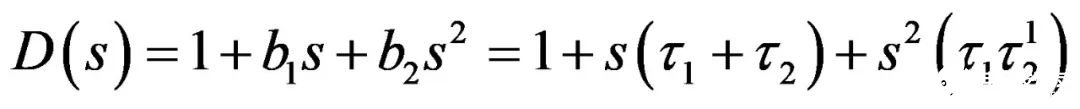
(14)
t1和t2是所有储能元件(C和Ls )保持在直流状态(电容开路,电感短路)时获得的时间常数。表示在时间常数1(上标数字)的元件处于高频状态(电容器短路,电感开路),同时确定在时间常数2的元件端的电阻。相反的,表示在时间常数2(上标数字)的元件处于高频状态(电容器短路,电感开路),同时确定时间常数1的元件端电阻。然后将这些时间常数组合,成为如(14)的D(s)。
首先,我们看看S=0时,储能元件端的电阻。在直流状态下,我们让所有电容开路和电感短路(如果有的话)。在开始任何类型的分析(.TRAN 或.AC)前,确定偏置点时,SPICE也同样这样做。我们想象如果我们移除电容器,输入端阻抗由Rinf决定,因此它的存在避免了无法衡量的项:
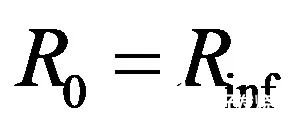
(15)
然后,我们确定每个电容器端提供的电阻R,而其对应于非直流状态(断开或从电路中移除)。我们绘制出图19。时间常数由t=RC定义。
您现在评估每个电容器端在直流状态(从电路中移除)时所提供的电阻。
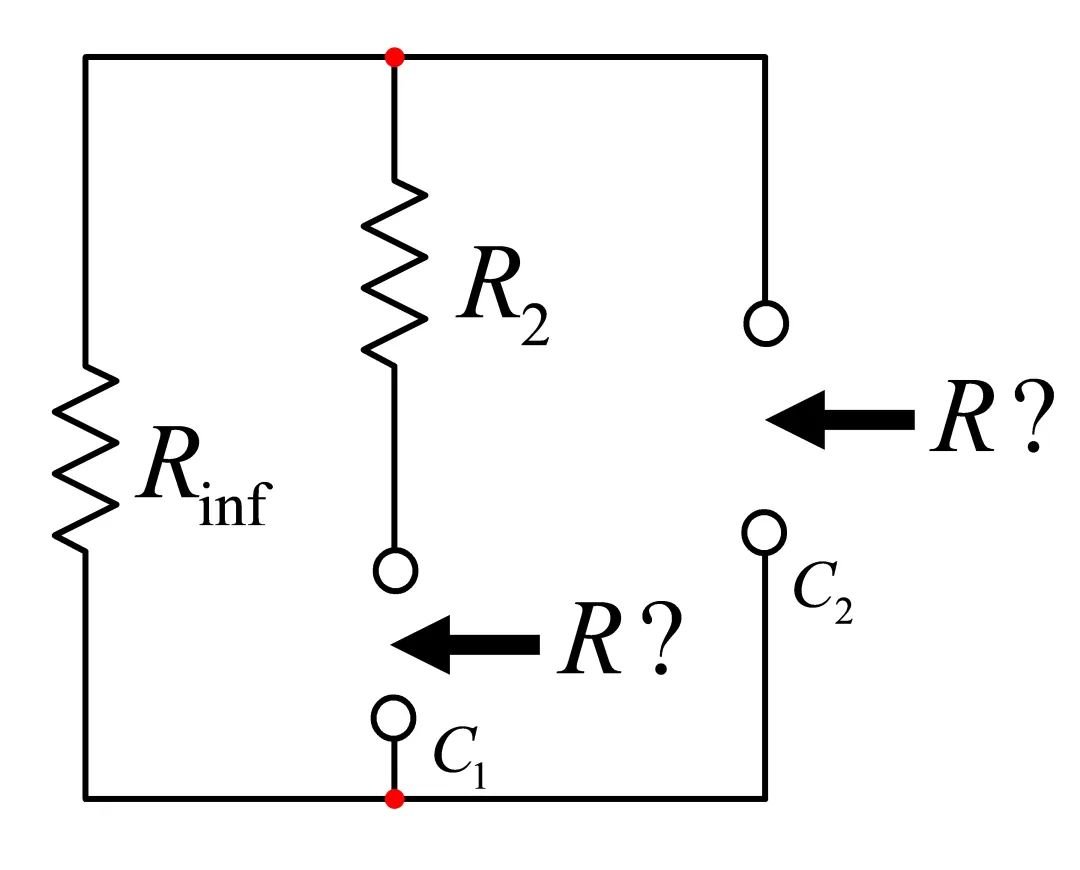
无需写一行代数,我们就可以检查图形和“得出”电容器端的电阻。我们有:
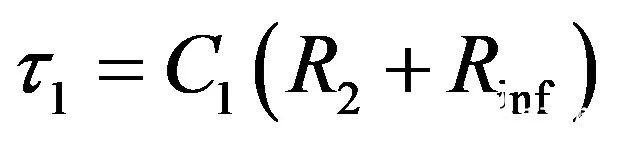
(16)
和
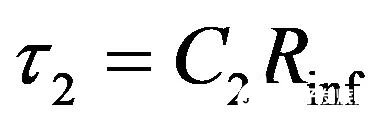
(17)
有了直流时间常数,让我们确定更高的频率,如图20所示。对于,电容C1短路,您看看电容C2端的阻抗。
电容C1短路,C2端的电阻是多少?
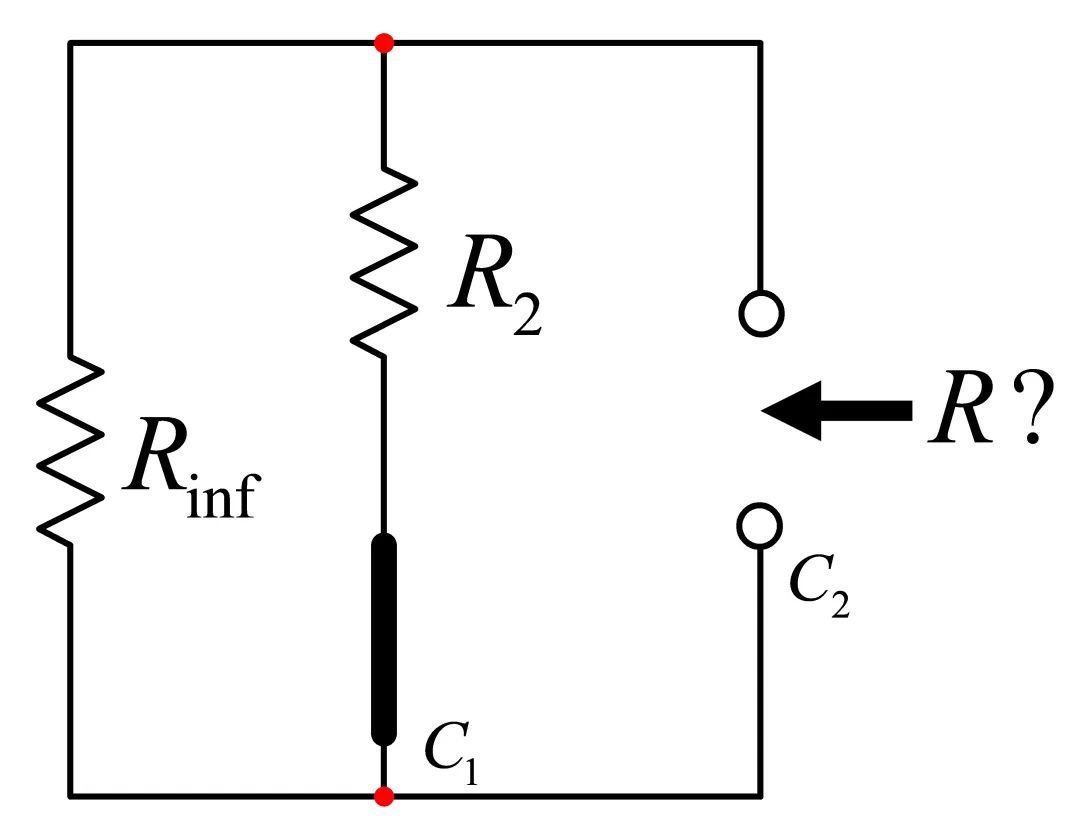
时间常数直接等于
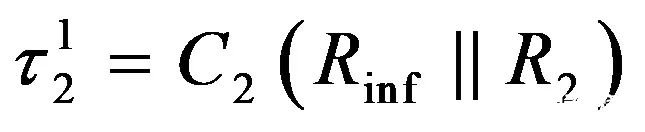
(18)
如果我们评估,将发现
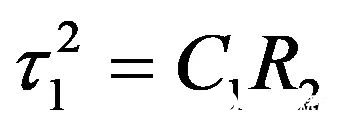
(19)
我们将所有项组合形成D(s):

(20)
分子可以通过检验得出。如果您还记得我在第一部分所说的,当一个特定的S值使变换后的回路无响应(即C替换1 / SC)时,会找到零点。响应是VT,由电流源测量。当VT变为0V,电路中一定出现了转换的短路。如果是这样,那么:
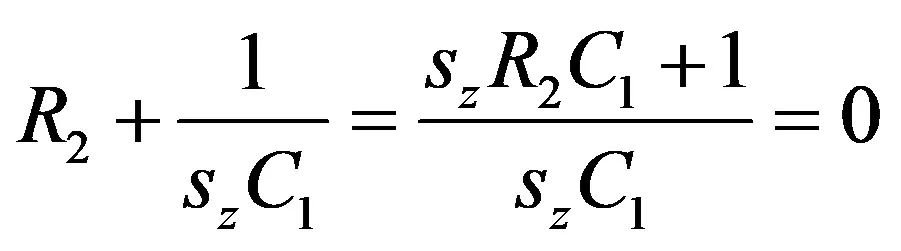
(21)
如果是这样,那么:
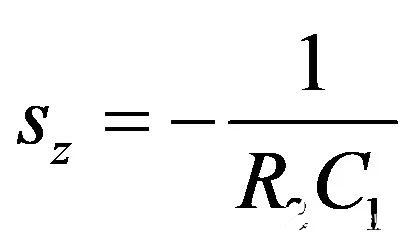
(22)
一切都已妥当,完整的传递函数如下所示:
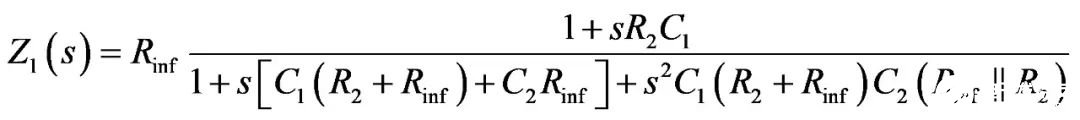
(23)
在分母中,提出Rinf,得到:
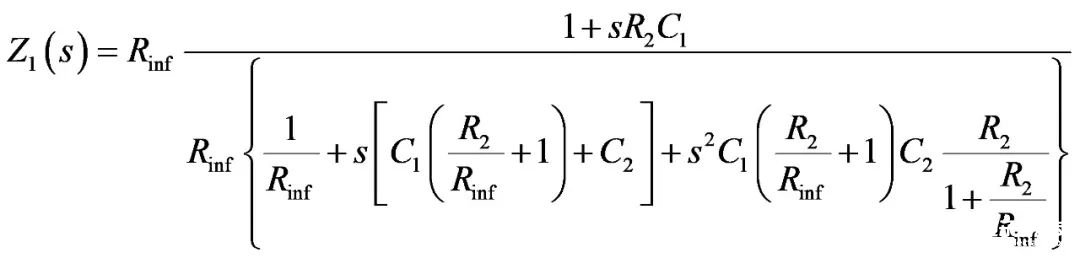
(24)
简化,令Rinf接近无穷大。最终的表达式为:
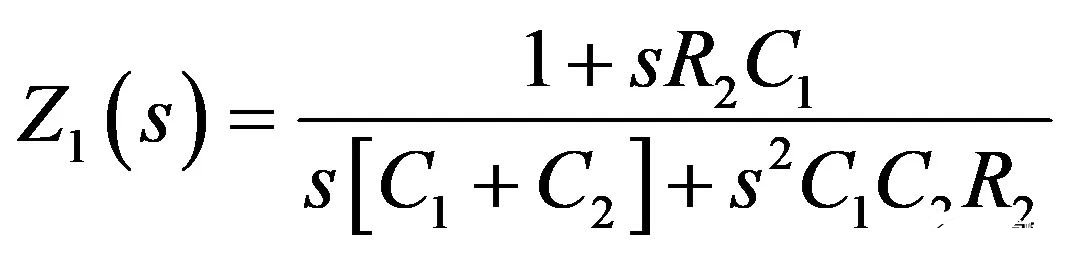
(25)
如果您现在将分子中的R2C1提出,会得出分子中有倒数的所谓的低熵表达式:
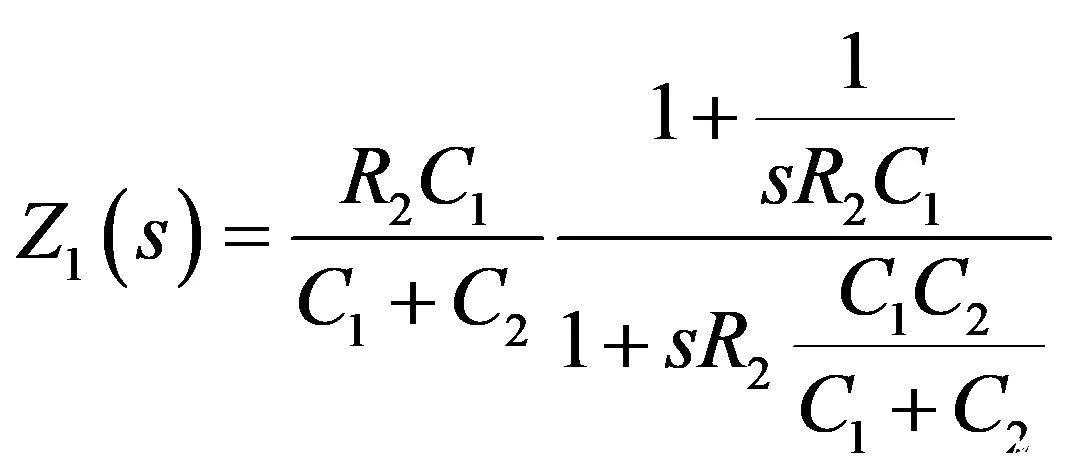
(26)
可用下列公式进一步调整:
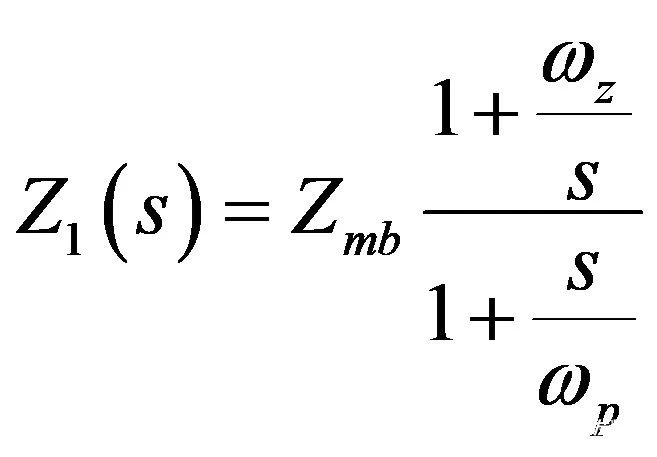
(27)
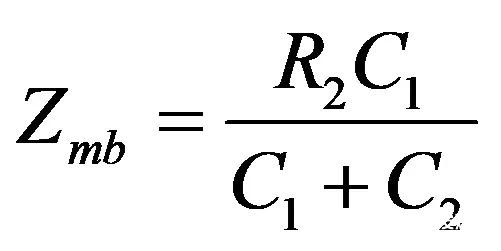
(28)
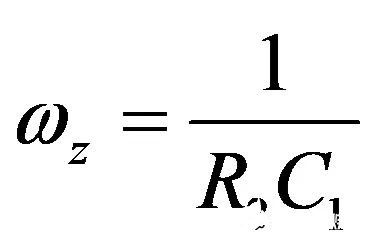
(29)
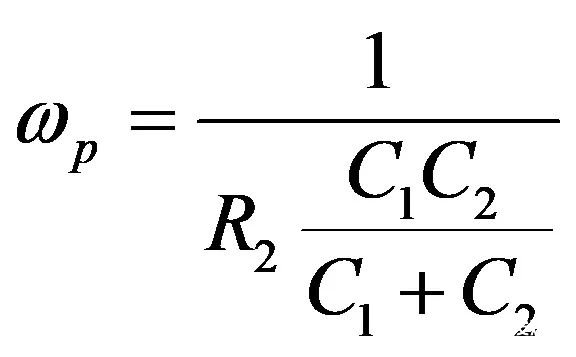
(30)
首项仍然含阻抗,但不再是S=0时的值。它是您在图21中看到的平坦区或中频带电阻,我们汇集所有表达式来测试它们的个别响应。它们都是相同的。
Mathcad确定原始表达式和最终表达式相同。
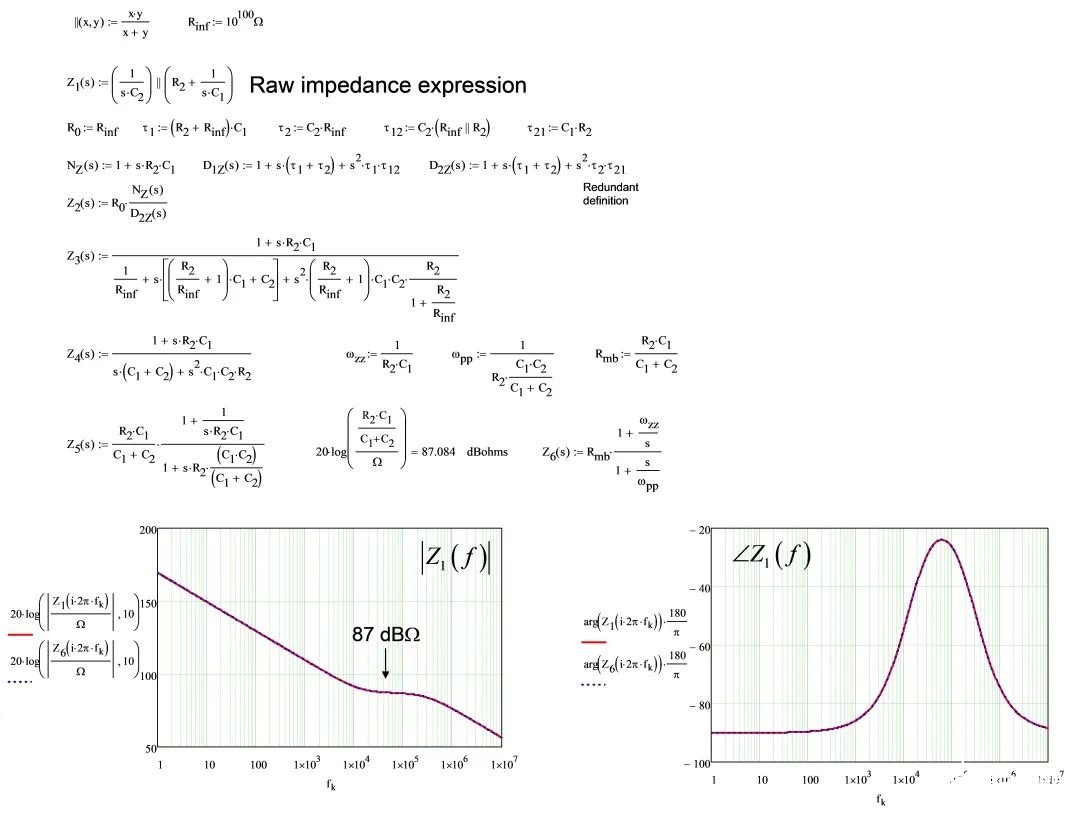
Raw impedance expression:原始阻抗表达式
快速分析电路技术展示了如何将电路分解成小的个别的草图,并单独处理每个草图。若可检测,很快就能得到结果,和得出有条有理的形式。这是这种方法的强大之处,我鼓励您掌握这技巧,因为在确定复杂的传递函数时,时间优势是很重要的。
为激发您的兴趣,请看图22。您看到一个type-3补偿器。无需写一行代数,我可以告诉您,当Z1和Z2分别转化为短路和开路时,响应VFB消失。(26)已评估了Z1,并提供一个零点,等于:
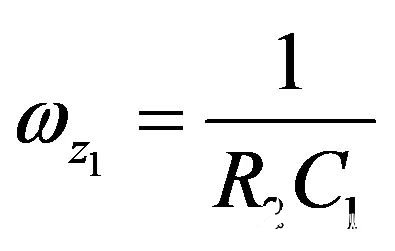
(31)
为了防止激励Vout形成响应VFB,还有个选择是Z2开路。换句话说,对于s=sz2,阻抗表达式不再有分母。
type-3电路是三阶有源滤波器
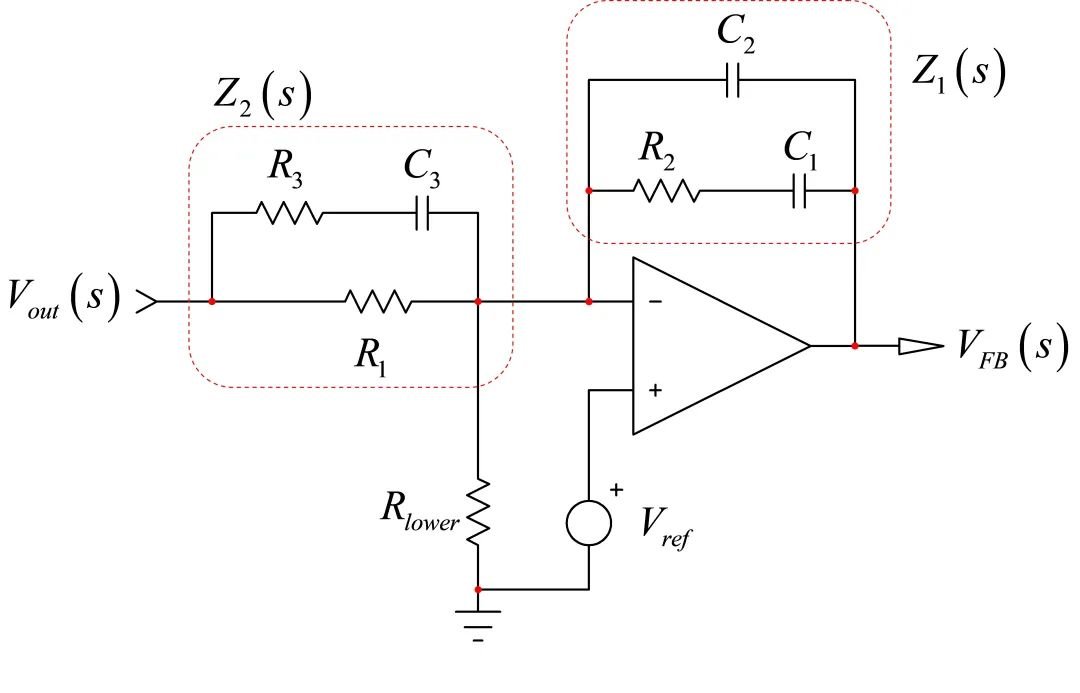
为确定Z2的阻抗(孤立于整个电路),我们可以想象一个电流源与R1并联。s=0时,您「看到」电流源两端的阻抗是R1(C3处于直流开路状态)。当激励(电流源)减至0A(一个0-A电流源从电路消失)时,时间常数是C3两端的电阻R,数倍于C3。简单地表示为。我们不需要分子,因为我们只对分母的根感兴趣。然而,如果您也想要分子,那么与我们分析Z1的架构相同。如果R3和C3短路,电流源的响应VT消失。只要组合这些数据,就有:
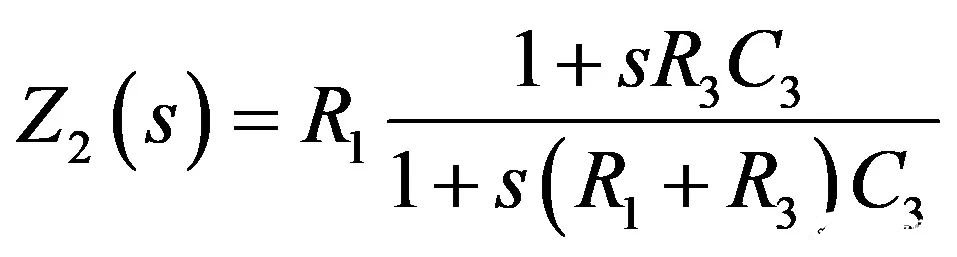
(32)
要取消分母,并让这个阻抗大小接近无穷大,您必须解得:
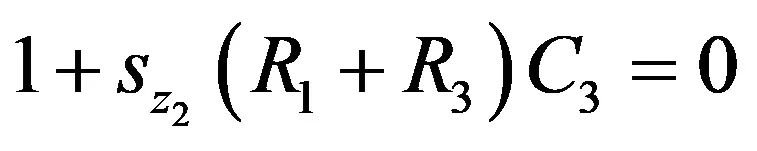
(33)
从而
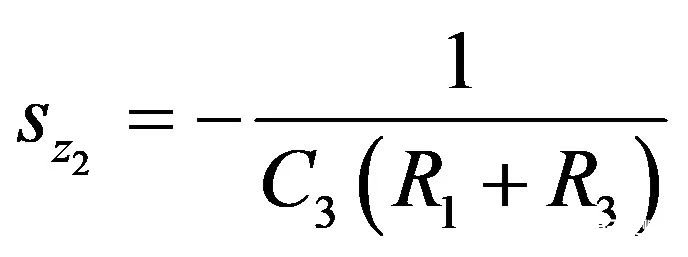
(34)
因此,起媒介作用的type 3传递函数是:
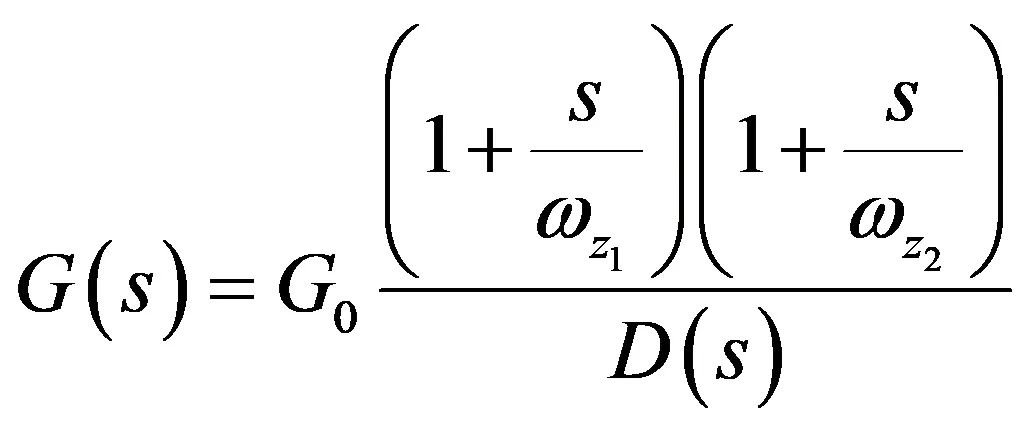
(35)
其中:
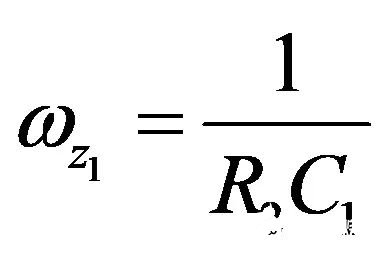
(36)
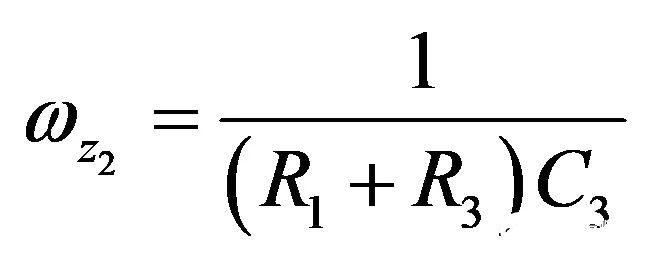
(37)
和